 Outil Optimisation
Outil Optimisation
Exigences relatives au rôle d'utilisateur
Rôle d'utilisateur* | Accès aux outils/fonctionnalités |
|---|---|
Utilisateur complet | ✓ |
Utilisateur de base | X |
*S'applique aux clients Alteryx OneÉditions Professional et Enterprise sur les versions 2025.1 et ultérieures de Designer.
L'outil Optimisation peut résoudre les problèmes d'optimisation de la programmation linéaire (LP), la programmation linéaire en nombres entiers mixtes (MILP) et la programmation quadratique (QP) à l'aide de modes d'entrée de fichier, de matrice et manuels.
Important
Cet outil n'est pas installé automatiquement avec Designer. Pour l'utiliser, téléchargez et installez les outils prédictifs Alteryx pour votre version de Alteryx Designer. En fonction de votre type de compte Alteryx, vous disposez de deux options de téléchargement :
Télécharger depuis Alteryx One
Télécharger depuis le portail des licences et téléchargements Alteryx.
Pour plus d'informations, consultez la page Télécharger et utiliser les outils prédictifs
Qu’est-ce que l’optimisation ?
L'optimisation a diverses applications dans de nombreux secteurs d'activité, par exemple les chaînes logistiques, le transport, les services financiers, la vente au détail, les télécommunications et l'énergie. Les domaines d’application incluent l’optimisation des chaînes logistiques, l’optimisation des assortiments, l’optimisation des portefeuilles, la planification de la main-d’œuvre et la programmation sportive.
Un problème d'optimisation se présente généralement sous la forme mathématique suivante, qui consiste en une fonction objectif (première équation), un ensemble de contraintes (deuxième équation), ainsi que la spécification des types (continu, entier, binaire) et des limites des variables de décision (troisième équation). Il convient généralement de trouver les valeurs des variables de décision qui optimisent ou minimisent l'objectif, tout en satisfaisant l'ensemble des contraintes, des types et des limites sous-jacents.
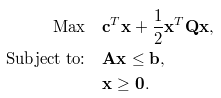
Connexion des entrées
Aucune entrée n’est requise pour les modes d’entrée de fichier ou manuel. Pour le mode d'entrée de matrice, les entrées O et A sont requises (les entrées B et Q sont facultatives). L'entrée B n'est facultative que dans certains cas. Vous ne pouvez pas toujours fournir les informations dans l'entrée A, uniquement si vous avez sélectionné des contraintes dans les lignes.
Ancrage O : (Obligatoire pour le mode d'entrée de matrice) Utilisez cette entrée pour indiquer le nom des variables de décision, leurs coefficients dans la fonction objectif et, éventuellement, leurs limites et leurs types.
Notez qu'en raison de la fonctionnalité R, les noms de champs sont sensibles à la casse. À partir de Designer 11.0, vous pouvez activer l'option Afficher l'affectation des champs de l'ancrage d'entrée O pour plus de flexibilité au niveau des noms de champs.
variable (Obligatoire) : chaîne, noms des variables de décision. Correspond à x dans les équations.
coefficient (Obligatoire) : valeur numérique, coefficient de chaque variable de décision dans une fonction objectif. Correspond à c.
lb (Facultatif) : valeur numérique, limite inférieure de la variable de décision. La valeur par défaut est 0.
ub (Facultatif) : valeur numérique, limite supérieure de la variable de décision. La valeur par défaut est Inf (infini positif).
type (Facultatif) : caractère, type de la variable de décision, qui peut être C (continu), B (binaire) ou I (entier). La valeur par défaut est C.
Ancrage A (Obligatoire pour le mode d'entrée de matrice) : utilisez cette entrée pour indiquer la matrice de contrainte correspondant à A dans les équations. Vous pouvez organiser la matrice de deux manières différentes :
Matrice dense :
Contraintes en lignes : chaque ligne correspond à une contrainte.
Si vous le souhaitez, vous pouvez nommer le premier champ contrainte pour indiquer le nom de contrainte dans chaque ligne, tandis que les autres noms de champs doivent correspondre aux variables de décision définies dans O.
En outre, vous pouvez inclure les champs dir et rhs afin d'y reporter l'entrée B dans l'entrée A.
dir : chaîne, direction de l'inégalité de contrainte. Ce champ doit être renseigné par >=, <= ou ==.
rhs : valeur numérique, côté droit de l'inégalité, correspondant à b.
Les champs de variable (x, y et z dans l'exemple ci-dessous) doivent être numériques.
L'ordre des colonnes doit correspondre à l'ordre des lignes pour l'entrée O.
Exemple : si vos équations de contrainte sont : x + 2y + 3z <= 4 et x + y >= 1, ce sont toutes des entrées légitimes pour l'entrée A:
Avec champ de contrainte :
contrainte
x
y
z
1
c1
1
2
3
2
c2
1
1
0
Sans champ de contrainte :
x
y
z
1
1
2
3
2
1
1
0
En incluant dir et rhs :
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
Variables en lignes : chaque ligne correspond à une variable.
Le premier champ doit être nommé variable, tandis que les autres noms de champs doivent correspondre aux noms de contraintes. Notez que cette information correspond à la transposition de la matrice A dans les équations ci-dessus.
Les champs de contrainte (c1 et c2 dans l'exemple ci-dessous) doivent être numériques.
L'ordre des variables des entrées O et A doit être identique.
Exemple : voici une entrée légitime pour l'entrée A :
variable
c1
c2
1
x
1
1
2
y
2
1
3
z
3
0
À partir de Designer 11.0, vous pouvez utiliser d'autres noms de champs pour « contrainte » ou « variable » et l'outil Optimisation déduit de manière intelligente quel champ contient des contraintes et quel autre contient des variables. Cependant, la convention de dénomination est toujours préférée et recommandée.
Matrice éparpillée : pour les ensembles de contraintes volumineux, vous pouvez spécifier la matrice A sous sa forme SLAM. Celle-ci consiste en trois champs obligatoires i, j et v, i et j correspondant aux index de lignes et de colonnes, respectivement, et v désignant la valeur non nulle de l'élément de matrice. Le mode Matrice éparpillée suppose toujours l’utilisation de contraintes en lignes.
Ancrage B : (Obligatoire si cette information n'est pas déjà indiquée dans A) : utilisez cette entrée pour indiquer le nom, la direction et le côté droit des contraintes.
contrainte (Facultatif) : chaîne, nom de la contrainte.
dir : chaîne, direction de l'inégalité de contrainte. Ce champ doit être renseigné par >=, <= ou ==.
rhs : valeur numérique, côté droit de l'inégalité, correspondant à b.
Ancrage Q (Facultatif) : utilisez cette entrée pour indiquer la partie quadratique de la fonction objectif en cas de problèmes de programmation quadratique. Cette entrée correspond à Q dans les équations. Vous pouvez la définir en tant que matrice dense ou matrice éparpillée.
Matrice dense : les noms de champs doivent correspondre aux noms des variables de décision définis dans O.
Matrice éparpillée : les noms de champs sont i, j et v, i et j correspondant aux index de lignes et de colonnes, respectivement, et v désignant la valeur non nulle de l'élément de matrice associé.
Modes d’entrée
Sélectionner le modèle comme matrices
Le mode Matrice prend en charge les matrices denses ou éparpillées (slam). Les entrées O et A sont requises pour le mode d'entrée Matrice.
Sélectionner le type de problème :
Programme linéaire : (Par défaut)(LP) Objectif linéaire et contraintes linéaires avec variables de décision continues.
Programmation en nombres entiers mixtes : (MILP) Objectif linéaire et contraintes linéaires avec variables de décision binaires ou entières ainsi que variables de décision continues.
Programmation quadratique : (QP) Objectif quadratique et contraintes linéaires avec variables de décision continues.
Sélectionner le solveur :
Glpk : (Par défaut) Pour les programmations linéaires et les programmations linéaires en nombres entiers mixtes.
Symphony : pour les programmations linéaires et les programmations en nombres entiers mixtes. Ce solveur est généralement plus efficace que Glpk pour les programmations MILP.
Quadprog : pour les programmes quadratiques.
Optimiser l'objectif ? : activez cette option si vous voulez optimiser la fonction objectif. Sinon, l’outil minimise la fonction objectif.
Sélectionner le mode de contrainte pour l'ancrage d'entrée A : pour plus de détails, voir Connexion des entrées ci-dessus.
Matrice dense, contraintes en lignes (Par défaut)
Matrice dense, variables en lignes
Matrice éparpillée (SLAM)
Mappage de champ d'affichage pour l'ancrage d'entrée O (facultatif) : l'entrée O nécessite les mots réservés variable, coefficient, lb, ub ou type pour les noms de champ de la table d'entrée. Si vous utilisez d’autres noms de champs ou si les noms de champs contiennent un espace vide en début ou en fin, des erreurs se produisent alors. En activant cette option, vous pouvez affecter les champs existants aux champs variable, coefficient, lb, ub et type correspondants sans avoir recours à l'étape supplémentaire consistant à utiliser un Outil Sélectionner pour modifier les noms de champs.
Entrer le modèle manuellement
Ce mode offre une interface interactive dans laquelle vous pouvez définir directement les objectifs et les contraintes. L’analyse de la sensibilité est disponible en cas de problèmes de programmation linéaire.
Sélectionner le type de problème :
Programmation linéaire : (Par défaut)(LP) Objectif linéaire et contraintes linéaires avec variables de décision continues.
Programmation en nombres entiers mixtes : (MILP) Objectif linéaire et contraintes linéaires avec variables de décision binaires ou entières ainsi que variables de décision continues.
Programmation quadratique : (QP) Objectif quadratique et contraintes linéaires avec variables de décision continues.
Sélectionner le solveur : Glpk (pour la programmation linéaire et la programmation en nombres entiers mixtes), Symphony (pour la programmation linéaire et la programmation en nombres entiers mixtes) ou Quadprog (pour la programmation quadratique).
Optimiser l'objectif ? : activez cette option si le problème est lié à l'optimisation.
Liste de variables : indiquez les noms des variables de décision dans une liste séparée par des virgules.
Objectif : indiquez la fonction objectif à optimiser ou minimiser.
Contraintes : spécifiez les contraintes. Assurez-vous que toutes les variables de la contrainte se trouvent à gauche du signe d'inégalité/égalité. (Par exemple, le solveur échoue pour la contrainte 2x>=y+4, mais s'exécute avec succès pour la contrainte 2x-y>=4. Bien que ces deux équations soient mathématiquement équivalentes, la deuxième satisfait aux exigences du solveur.)
Bounds & Types: Specify the bounds and types.
Indiquer le modèle à partir d'un fichier
Ce mode prend en charge l'entrée de fichier de modèle standard.
Sélectionnez le type de fichier : CLPEX_LP, MathProg ou MPS_Free.
Sélectionner le solveur : Glpk (pour la programmation linéaire et la programmation en nombres entiers mixtes), Symphony (pour la programmation linéaire et la programmation en nombres entiers mixtes) ou Quadprog (pour la programmation quadratique).
Sélectionner un fichier : spécifiez un fichier de modèle d'optimisation.
Visualisation de la sortie
Ancrage I : cette sortie fournit un tableau de bord récapitulatif interactif de la solution.
Ancrage D : cette sortie se compose de 3 tables séparées par des tubes : résumé, variables et contraintes. Ces éléments peuvent être utilisés en amont du workflow pour créer des rapports et des tableaux récapitulatifs.
Ancrage S : il s'agit d'une sortie de données simple consistant en une table unique contenant la valeur optimale de la fonction objectif et les variables de décision. En cas de problèmes consistant en des variables de décision binaires uniquement (0/1), cette table ne contient que les valeurs 1.
