 Herramienta Optimización
Herramienta Optimización
Requisitos del rol de usuario
Rol de usuario* | Acceso a herramientas/características |
|---|---|
Usuario completo | ✓ |
Usuario básico | X |
* Se aplica a los clientes de las ediciones profesional y empresarial de Alteryx One en las versiones 2025.1 o posteriores de Designer.
La herramienta Optimización resuelve problemas de optimización de programación lineal (LP), programación lineal de enteros mixtos (MILP) y programación cuadrática (QP) utilizando los modos de entrada de matrices, manual y de archivos.
Importante
Esta herramienta no se instala automáticamente con Designer. Para utilizarlo, descarga e instala las herramientas predictivas de Alteryx para tu versión de Alteryx Designer. Dependiendo del tipo de cuenta de Alteryx, tienes dos opciones de descarga:
Descargar desde Alteryx One
Descargar desde el Portal de descargas y licencias de Alteryx.
Para obtener más información, ve a Descargar y usar herramientas predictivas.
¿Qué es la optimización?
La optimización tiene amplias aplicaciones en muchas industrias, como la cadena de suministro, el transporte, los servicios financieros, el comercio minorista, las telecomunicaciones y la energía. Las áreas de aplicación incluyen la optimización de la cadena de suministro, la optimización del surtido, la optimización de cartera, la programación de la fuerza de trabajo y la programación deportiva.
Por lo general, un problema de optimización tiene la siguiente forma matemática, que consiste en una función objetiva (primera ecuación), un conjunto de restricciones (segunda ecuación), y una especificación de los tipos (continuo, entero, binario) y los límites de las variables de decisión (tercera ecuación). El objetivo es generalmente encontrar los valores de las variables de decisión que maximizan o minimizan el objetivo mientras satisfacen todas las restricciones subyacentes, tipos y límites.
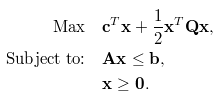
Conectar entradas
No se requieren entradas para los modos de entrada manual o de archivo. Para el modo de entrada de matriz, se requieren entradas O y A, pero las entradas B y Q son opcionales. La entrada B solo es opcional en algunos casos. No siempre se puede proporcionar la información en la entrada A, solo si has seleccionado restricciones en las filas.
Ancla O: (requerido para el modo de entrada de matriz) usa esta entrada para proporcionar los nombres de las variables de decisión, sus coeficientes en la función objetivo y, opcionalmente, sus límites y tipos.
Ten en cuenta que debido a la funcionalidad R, los nombres de los campos distinguen entre mayúsculas y minúsculas. A partir de Designer 11.0, puedes habilitar la opción Mostrar asignación de campos para un ancla de entrada O para mayor flexibilidad con los nombres de campos.
variable (requerido): una cadena, nombres de variables de decisión. Corresponde a x en las ecuaciones.
coeficiente (requerido): un número, coeficiente de cada variable de decisión en función objetiva. Corresponde a c.
lb (opcional): un número, límite inferior de la variable de decisión. El valor predeterminado es 0.
ub (opcional): un número, límite superior de la variable de decisión. El valor predeterminado es Inf (infinito positivo).
tipo (opcional): un carácter, el tipo de la variable de decisión, que puede ser C (continuo), B (binario) o I (entero). El valor predeterminado es C.
Ancla A (necesario para el modo de entrada de matriz): utiliza esta entrada para proporcionar la matriz de restricción correspondiente a A en las ecuaciones. Puedes organizar la matriz de dos maneras diferentes:
Matriz densa:
Restricciones en filas: cada fila corresponde a una restricción.
El primer campo se puede llamar de forma opcional como restricción para indicar el nombre de la restricción en cada fila, mientras que los nombres de campo restantes deben corresponder a las variables de decisión definidas en O.
Además, puedes incluir los campos dir y rhs para combinar la entrada B en la entrada A.
dir: una cadena, dirección de la inequidad de restricción. Tiene que ser >=, <= o ==.
rhs: un número, el lado derecho de la inequidad, correspondiente a b.
Los campos variables (x, y, y z en el ejemplo siguiente) deben ser numéricos.
El orden de las columnas debe coincidir con el orden de las filas para la entrada O.
Ejemplo: si las ecuaciones de restricción son: x + 2y + 3z <= 4 y x + y >= 1,, todas son entradas legítimas para la entrada A:
Con campo de restricción:
restricción
x
y
z
1
c1
1
2
3
2
c2
1
1
0
Sin campo de restricción:
x
y
z
1
1
2
3
2
1
1
0
Incluidos dir y rhs:
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
Variables en filas: cada fila corresponde a una variable.
El primer campo debe llamarse variable, mientras que los nombres de campo restantes deben corresponder a los nombres de la restricción. Ten en cuenta que esto corresponde a la transposición de la matriz A en las ecuaciones anteriores.
Los campos de restricción (c1 y c2 en el ejemplo de abajo) deben ser numéricos.
El orden de las variables de entrada O y entrada Adebe ser el mismo.
Ejemplo: esta es una entrada legítima para la entrada A:
variable
c1
c2
1
x
1
1
2
y
2
1
3
z
3
0
A partir de Designer 11.0, puedes usar otros nombres de campo para “restricción” o “variable” y la herramienta Optimización deduce de forma inteligente qué campo contiene restricciones y qué campo contiene variables. Sin embargo, la convención de nomenclatura sigue siendo preferible y recomendada.
Matriz poco densa: para conjuntos de restricciones más grandes, puedes especificar la matriz A en su forma SLAM. Consta de tres campos requeridos i, j y v, donde i y j son índices de fila y columna, respectivamente, y v es el valor distinto de cero del elemento matriz. El modo de matriz poco densa siempre asume restricciones en las filas.
Ancla B (requerida si no está ya provista en A): usa esta entrada para proporcionar el nombre, la dirección y el lado derecho de las restricciones.
restricción (opcional): una cadena, nombre de la restricción.
dir: una cadena, dirección de la inequidad de restricción Tiene que ser >=, <= o ==.
rhs: un número, el lado derecho de la inequidad, correspondiente a b.
Ancla Q (opcional): usa esta entrada para proporcionar la parte cuadrática de la función objetiva, para problemas de programación cuadrática. Corresponde a Q en las ecuaciones. Puedes especificarlo como una matriz densa o como una matriz poco densa.
Matriz densa: los nombres de los campos deben corresponder a los nombres de las variables de decisión definidos en O.
Matriz poco densa: los nombres de los campos son i, j y v, donde i y j son índices de fila y columna, respectivamente, y v es el valor distinto de cero del elemento matriz asociado.
Modos de entrada
Seleccione el modelo como matrices
El modo Matriz es compatible con matrices densas o poco densas (slam). Las entradas O y A son necesarias para el modo Entrada de matriz.
Seleccionar el tipo de problema:
Programa lineal: (predeterminado) (LP) restricciones lineales objetivas y lineales con variables de decisión continuas.
Programa de enteros mixtos: (MILP) restricciones lineales objetivas y lineales con variables de decisión binarias o enteras junto con variables de decisión continuas.
Programa cuadrático: (QP) restricciones objetivas y lineales cuadráticas con variables de decisión continua.
Seleccionar solucionador:
Glpk: (predeterminado) para programas lineales y programas lineales enteros mixtos.
Symphony: para programas lineales y programas enteros mixtos. Generalmente funciona mejor que Glpk para MILP.
Quadprog: para programas cuadráticos.
¿Maximizar objetivo?: habilita esta opción si deseas maximizar la función objetiva. De lo contrario, la herramienta minimiza la función objetiva.
Seleccionar modo de restricciones para el ancla de entrada A: para obtener más detalles, consulta Conectar entradas arriba.
Matriz densa, restricciones en filas (predeterminada)
Matriz densa, variables en columna
Matriz poco densa (SLAM)
Mostrar la asignación de campos para un Ancla de entrada O(opcional): la entrada O requiere las palabras reservadas variable, coefficient, lb, ub o type para los nombres de campos de la tabla de entrada. Si utilizas nombres de campos diferentes, o si los nombres de los campos contienen espacios en blanco al principio o al final, se producen errores. Al habilitar esta opción, puedes asignar tus campos existentes a los campos variable, coeficiente, lb, ub y tipo correspondientes sin el paso adicional de usar una herramienta Seleccionar para cambiar los nombres de los campos.
Introducir el modelo manualmente
Este modo ofrece una interfaz interactiva donde puedes especificar objetivos y restricciones directamente. El análisis de sensibilidad está disponible para problemas de programación lineal.
Seleccionar el tipo de problema:
Programa lineal: (LP) restricciones lineales objetivas y lineales con variables de decisión continuas.
Programa de enteros mixtos: (MILP) restricciones lineales objetivas y lineales con variables de decisión binarias o enteras junto con variables de decisión continuas.
Programa cuadrático: (QP) restricciones objetivas y lineales cuadráticas con variables de decisión continua.
Seleccionar solucionador: Glpk (para programa lineal y programa entero mixto), Symphony (para programa lineal y programa entero mixto), o Quadprog (para programa cuadrático).
¿Maximizar objetivo?: activa esta opción si se trata de un problema de maximización.
Lista de variables: especifica una lista separada por comas de nombres de variables de decisión.
Objective (Objetivo): especifica una función objetiva que se debe maximizar o minimizar.
Constraints (Restricciones): especifica las restricciones. Asegúrate de que todas las variables de la restricción estén en el lado izquierdo del signo de inequidad/equidad. (Por ejemplo, el solucionador falla para la restricción 2x>=y+4 pero se ejecuta correctamente para la restricción 2x-y>=4. Mientras que ambas ecuaciones son matemáticamente equivalentes, la segunda cumple con los requisitos del solucionador).
Bounds & Types: Specify the bounds and types.
Especificar el modelo desde un archivo
Este modo soporta la entrada de archivo modelo estándar de la industria.
Seleccionar el tipo de archivo: CLPEX_LP, MathProg o MPS_Free.
Seleccionar solucionador: Glpk (para programa lineal y programa entero mixto), Symphony (para programa lineal y programa entero mixto), o Quadprog (para programa cuadrático).
Seleccionar archivo: especifica un archivo de modelo de optimización.
Ver la salida
Ancla I: esta salida proporciona un panel de control interactivo de la solución.
Ancla D: esta salida consta de tres tablas separadas por plecas (resumen, variables y restricciones). Se pueden utilizar en las etapas iniciales del flujo de trabajo para crear informes y paneles.
Ancla S: se trata de una salida de datos simple que consiste en una sola tabla con el valor óptimo de la función objetiva y las variables de decisión. Para los problemas que consisten solo en variables de decisión binaria (0/1), esta tabla contiene solo aquellos valores que son 1.
